二、极化现象

二、极化现象#

1. 极化信道及其容量#

1.1 一层极化#

回顾上一节，我们引入了一类被称为“极化信道”的特殊信道：\(W_N^{(i)}\)。它以第\(i\)个随机变量\(U_i\)为输入，以前\(i-1\)个随机变量\(U_{1:i-1}\)和随机变量\(Y_{1:N}\)为输出，在码长为\(N\)时，共有\(N\)个这样的信道。首先我们考虑码长为\(2\)的情况：

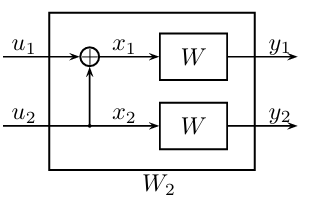
码长为2的极化码

上图中有两个极化信道：

\(W_2^{(1)}\)，以\(U_1\)为输入，以\(Y_1,Y_2\)为输出；
\(W_2^{(2)}\)，以\(U_2\)为输入，以\(Y_1,Y_2,U_1\)为输出。

极化信道的定义是十分抽象的，请接受它。

由于这个场景比较简单，我们可以直接写出两个极化信道的转移概率矩阵。设简单信道\(W\)为一比特翻转信道，翻转概率为\(p\)。那么第一个极化信道的转移概率矩阵为：

\(W_2^{(1)}\)	\((y_1,y_2)=(0,0)\)	\((y_1,y_2)=(0,1)\)	\((y_1,y_2)=(1,0)\)	\((y_1,y_2)=(1,1)\)
\(u_1=0\)	\(\frac{1}{2}(1-p)^2+\frac{1}{2}p^2\)	\(p\cdot(1-p)\)	\(p\cdot(1-p)\)	\(\frac{1}{2}(1-p)^2+\frac{1}{2}p^2\)
\(u_1=1\)	\(p\cdot(1-p)\)	\(\frac{1}{2}(1-p)^2+\frac{1}{2}p^2\)	\(\frac{1}{2}(1-p)^2+\frac{1}{2}p^2\)	\(p\cdot(1-p)\)

当\(p=0.1\)时，代入计算其信道容量可得\(I(W_2^{(1)}) = 0.3199\)。

第二个极化信道的转移概率矩阵为：

\(W_2^{(2)}\)	\((y_1,y_2,u_1)=(0,0,0)\)	\((y_1,y_2,u_1)=(0,0,1)\)	\((y_1,y_2,u_1)=(1,0,0)\)	\((y_1,y_2,u_1)=(1,0,1)\)	\((y_1,y_2,u_1)=(0,1,0)\)	\((y_1,y_2,u_1)=(0,1,1)\)	\((y_1,y_2,u_1)=(1,1,0)\)	\((y_1,y_2,u_1)=(1,1,1)\)
\(u_2=0\)	\(\frac{1}{2}(1-p)^2\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}(1-p)^2\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}p^2\)	\(\frac{1}{2}p^2\)	\(\frac{1}{2}p(1-p)\)
\(u_2=1\)	\(\frac{1}{2}p^2\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}p^2\)	\(\frac{1}{2}p(1-p)\)	\(\frac{1}{2}(1-p)^2\)	\(\frac{1}{2}(1-p)^2\)	\(\frac{1}{2}p(1-p)\)

当\(p=0.1\)时，代入计算其信道容量可得\(I(W_2^{(2)}) = 0.7421\)。计算原信道\(W\)的容量为\(I(W)=0.5310\)，我们可以发现两个特点：

\(I(W_2^{(1)}) < I(W) < I(W_2^{(2)})\)，两个新信道的容量相对于原信道发生了定向偏移；
\(I(W_2^{(1)}) + I(W_2^{(2)}) = 2\cdot I(W)\)，信道容量总量保持不变。

第一个式子更严谨的形式其实是小于等于，第二个式子则是互信息链式法则的体现：

\[2\cdot\underbrace{I(X;Y)}_{I(W)}=I(Y_{1:2};X_{1:2})=I(Y_{1:2};U_{1:2})=\underbrace{I(Y_{1:2};U_1)}_{I(W_2^{(1)})}+\underbrace{I(Y_{1:2},U_1;U_2)}_{I(W_2^{(2)})}\]

1.2 两层极化#

当码长增加到\(N=4\)时，我们首先对四个简单信道\(W\)两两进行一层极化变换，从而得到四个“一阶”极化信道：

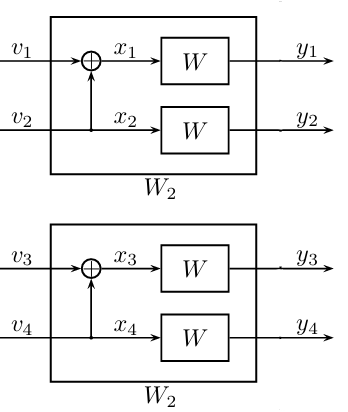
码长为4的极化码-一层极化

这四个“一阶”极化信道的输入输出分别为：

输入\(V_1\)，输出\(Y_1,Y_2\)；
输入\(V_2\)，输出\(Y_1,Y_2,V_1\)；
输入\(V_3\)，输出\(Y_3,Y_4\)；
输入\(V_4\)，输出\(Y_3,Y_4,V_3\)。

注意到，分别以\(v_1\)和\(v_3\)为输入的两个极化信道，它们同属于第一种“一阶”极化信道\(W_2^{(1)}\)，而分别以\(v_2\)和\(v_4\)为输入的两个极化信道，它们同属于第二种“一阶”极化信道\(W_2^{(2)}\)。基于这一相同点我们将它们分为两组，然后组内再进行一层极化变换，得到四个极化信道：

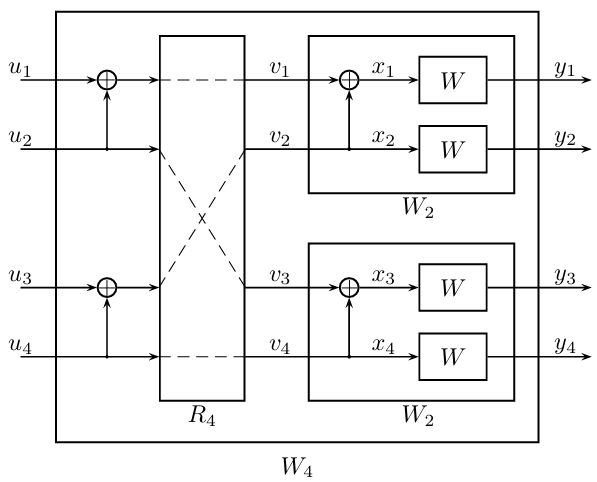
码长为4的极化码-两层极化

这四个极化信道分别为：

\(W_4^{(1)}\)，输入\(U_1\)，输出\(Y_{1:4}\)；
\(W_4^{(2)}\)，输入\(U_2\)，输出\(Y_{1:4},U_1\)；
\(W_4^{(3)}\)，输入\(U_3\)，输出\(Y_{1:4},U_{1:2}\)；
\(W_4^{(4)}\)，输入\(U_4\)，输出\(Y_{1:4},U_{1:3}\)。

这个过程可以推广到\(N=2^n\)的情况，根据互信息的链式法则，它们的容量之和为：

\[\sum_{i=1}^{N}I(Y_{1:N},U_{1:i-1};U_i)=N\cdot I(X;Y)\]

1.3 信道极化定理#

对所有的二进制输入离散无记忆信道（B-DMC）\(W\)而言，极化信道\(W^{(i)}_N\)按照如下规则发生极化：任意给定\(\delta\in(0,1)\)，当\(N\)按照\(2\)的整数次幂趋于无穷时，满足\(I(W_N^{(i)})\in(1-\delta,1]\)的索引\(i\)的占比趋近于\(I(W)\)，满足\(I(W_N^{(i)})\in[0,\delta)\)的索引\(i\)的占比趋近于\(1-I(W)\)。

这个定理可以粗略理解为，链式法则等式中，那些特殊形式的互信息要么是0要么是1，而位于0和1之间的项虽然也存在，但随着码长趋于无穷而占比趋于0。

占比趋于0，不代表数量趋于0。

2. 数学预备知识#

2.1 极化二叉树#

根据之前的叙述我们可以发现，在每一层极化变换后，极化信道的种类数都将翻倍，同一类的极化信道具有相同的结构和容量。因此，对码长为\(N=2^n\)进行\(n\)次极化构造的过程可以表示一个二叉树：

极化过程

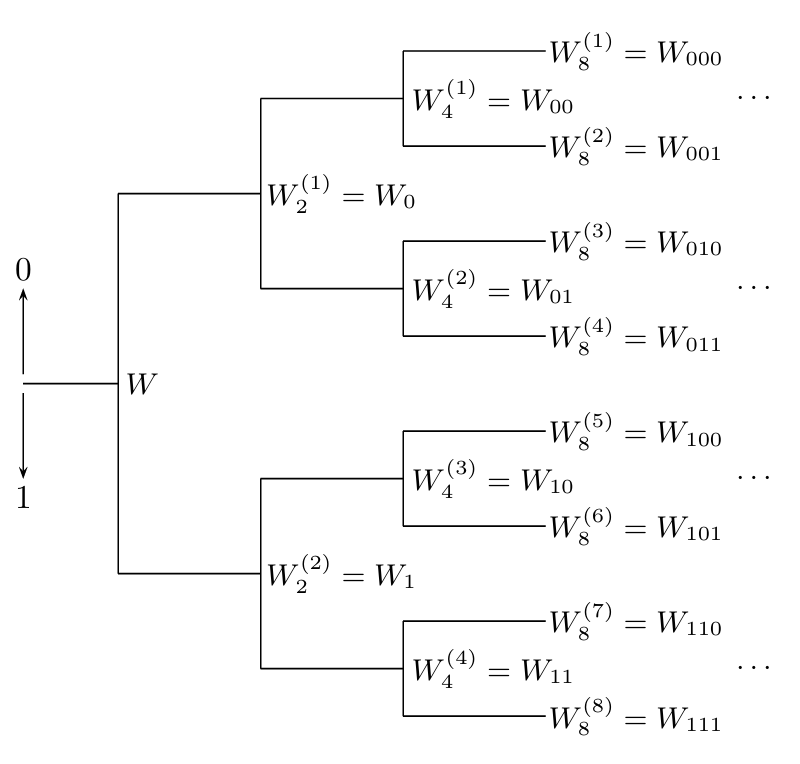
这个树上的每个节点\(W_N^{(i)}\)，在下一层都会分裂为两个新节点\(W_{2N}^{(2i-1)}\)和\(W_{2N}^{(2i)}\)，并且有：

\(I(W_{2N}^{(2i-1)})+I(W_{2N}^{(2i)})=2\cdot I(W_N^{(i)})\)

接下来我们考虑一个类似高尔顿板的结构，从根节点出发，在每个节点上随机选择一个子节点继续前进，一直进行下去。容易知道，在第\(n\)步中，当前节点对应的极化信道容量是一个随机变量，这个不断前进的过程是一个随机过程。

高尔顿板，将小球从顶层小口投入，在每个拐点处均匀随机向左向右下落，最终形成高斯分布包络线。是一种用于教学演示的常用装置。

对于一般意义上的B-DMC而言，极化二叉树各节点的值是难以计算的，信道容量\(I(W)\)并没有一个通用的简单递归式，不过BEC信道是一个例外。经过简单推导可以知道，若\(W\)的擦除概率为\(e\)，则分裂出的两个新信道的容量分别为\(e^2\)和\(2e-e^2\)。我们以\(e=0.5\)为例，简单绘制一下该随机过程在前几步的演化情况：

import numpy as np
from matplotlib import pyplot as plt

# 演化函数
def evolute(index: int, step: int, seqs: np.ndarray):
    for i in range(step):
        if index % 2 == 0:
            seqs[i + 1] = seqs[i] ** 2
        else:
            seqs[i + 1] = 2 * seqs[i] - seqs[i] ** 2
        index = (index >> 1)

# 初始化参数
e, n = 0.5, 10
Ws = np.empty((n + 1,))
Ws[0] = e
plt.figure(figsize=(8, 4))
# 生成所有可能的随机过程
for i in range(1 << n):
    evolute(i, n, Ws)
    plt.plot(np.arange(n + 1), Ws, "k", linewidth=0.1)
plt.grid()
plt.show()

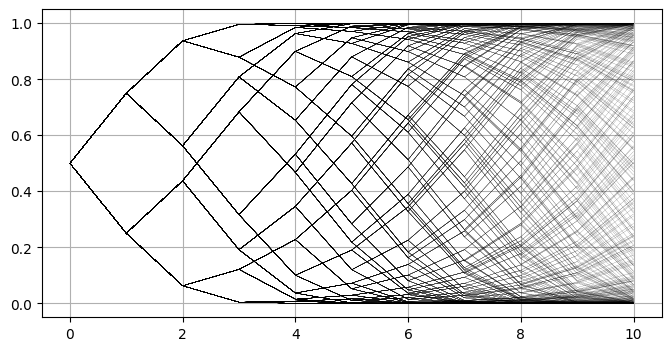
../_images/a291fc7bd5e66ec2e8436e9a5ce71a382e9aa8c6666a738e6c4acaeb1495f0cd.png

从上图可以粗略看出，随着步数逐渐增多，靠近边界上的路径密度越来越高。为了在更大步数下验证这个猜想，我们采用Monte-Carlo法均匀随机选择几条路径进行绘制：

e, n = 0.5, 20
Ws = np.empty((n + 1,))
Ws[0] = e
plt.figure(figsize=(12, 4))
# 均匀随机选择100条可能的路径
for i in np.random.randint(0, (1 << n), size=(100,)):
    evolute(i, n, Ws)
    plt.plot(np.arange(n + 1), Ws, linewidth=1)
plt.grid()
plt.show()

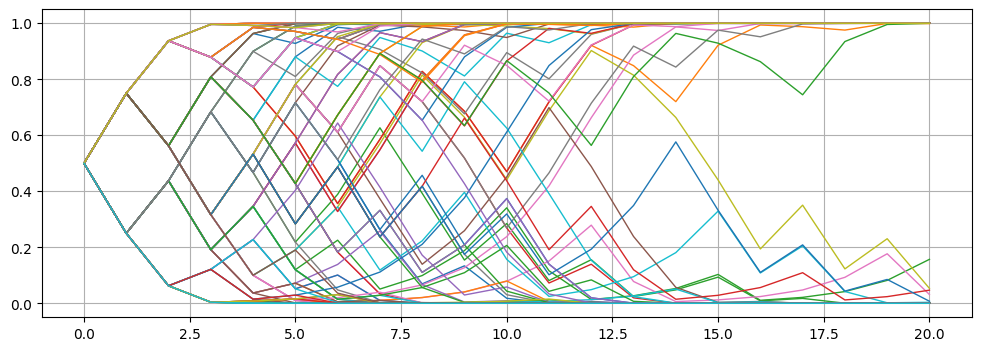
../_images/6a87a07804060c7b38a0e842fd2f2c1f1398eec87f71f7ec3b04ce3e1002e682.png

仿真结果验证了我们的猜想，随着步数逐渐增加，几乎所有路径的“尾巴”最终都将贴近0或1。这其实是个很深刻的现象，下一小节我们将从数学上对它做出更严格的描述。

2.2 鞅论基础#

极化二叉树所描述的随机过程，有一个关键的性质：在已知第\(n\)步的取值为\(I(W_N^{(i)})\)的条件下，第\(n+1\)步取值的条件期望就是\(I(W_N^{(i)})\)。在随机过程理论中，具有这种特性的随机过程被称为：鞅（Martingale）。

鞅：设\(\{X_n,n\geq 0\}\)和\(\{Y_n,n\geq 0\}\)是随机过程，对任意的\(n\geq 0\)，\(X_n\)是\(Y_0,\ldots,Y_n\)的函数，\(E|X_n|<\infty\)，且：

\[E(X_{n+1}|Y_0,\ldots,Y_n)=X_n,\forall n\geq 0\]

则称\(\{X_n\}\)是关于\(\{Y_n\}\)的鞅。

“随机过程在某一步的条件期望”与“随机过程在某一步的数学期望”是两个不同的概念，条件期望是关于条件部分的函数，而数学期望等于条件期望关于条件部分的均值。

上面关于鞅的定义至少还是能看懂的，但这种初级的措辞无法支撑更高级的应用。为了能看懂Arikan的证明过程，我们还需要在下面列出其他关键概念。

本小节只是对基本概念的简单列举，如果有兴趣深入研究，可参考北大数科讲义：应用随机过程。

\(\sigma\)代数：设\(\Omega\)是一个样本空间（或任意一个非空集合），\(\mathcal{F}\)是\(\Omega\)的某些子集组成的集合族，且满足如下特殊性质：

\(\Omega\in\mathcal{F}\)；
若\(A\in\mathcal{F}\)，则\(A^c\in\mathcal{F}\)；
若\(A_n\in\mathcal{F},n=1,2,\ldots\)，则\(\bigcup_n A_n\in\mathcal{F}\)。

则称\(\mathcal{F}\)为\(\Omega\)上的一个\(\sigma\)代数，而\((\Omega,\mathcal{F})\)称为可测空间，\(\mathcal{F}\)中的元素称为随机事件。

\(\sigma\)代数流与适应列：设\((\Omega,\mathcal{F},P)\)是完备的概率空间，若\(\{\mathcal{F}_n,n=0,1,\ldots\}\)是\(\mathcal{F}\)内的一系列满足\(\mathcal{F}_n\subset\mathcal{F}_{n+1}\)的子\(\sigma\)代数，则称之为\(\sigma\)代数流。如果\(\forall n\geq 0\)，\(X_n\)是\(\mathcal{F}_n\)可测的，则称随机过程\(\{X_n\}\)为\(\{\mathcal{F}_n\}\)适应的。

鞅的另一个定义：设\(\{\mathcal{F}_n,n\geq 0\}\)是\(\mathcal{F}\)中的一个\(\sigma\)代数流，如果随机过程\(\{X_n,n\geq 0\}\)是\(\{\mathcal{F}_n\}\)适应的，并且有：

\[E|X_n|\leq\infty,E(X_{n+1}|\mathcal{F}_n)=X_n\]

则称\(\{X_n\}\)是关于\(\{\mathcal{F}_n\}\)的鞅。

鞅收敛定理：设\(\{X_n\}\)是关于\(\{\mathcal{F}_n\}\)的鞅，并且存在常数\(C\)使得\(E|X_n|\leq C\)总成立，则当\(n\to \infty\)时，\(\{X_n\}\)几乎必然（almost surely, a.s.）收敛到一个随机变量\(X_\infty\)。

Borel \(\sigma\)代数：设\(\Omega=\mathbb{R}\)，由所有半无限区间\((-\infty,x]\)生成的\(\sigma\)代数，称为\(\mathbb{R}\)上的Borel \(\sigma\)代数，其中的元素称为Borel集合。

3. Arikan的证明#

3.1 Bhattacharyya参数#

记信道\(W\)输入\(x\)输出\(y\)的概率为\(W(y|x)\)，输入取值于集合\(\mathcal{X}\)，输出取值于集合\(\mathcal{Y}\)，则该信道的Bhattacharyya参数为：

\[Z(W)\triangleq \sum_{y\in\mathcal{Y}}\sqrt{W(y|0)W(y|1)}\]

该信道的对称容量为：

\[I(W)\triangleq \sum_{y\in\mathcal{Y}}\sum_{x\in\mathcal{X}}\frac{1}{2}W(y|x)\log{\frac{W(y|x)}{\frac{1}{2}W(y|0)\frac{1}{2}W(y|1)}}\]

对任意的二进制输入离散无记忆对称信道而言，有如下两个关系成立：

\(I(W)\geq\log{\frac{2}{1+Z(W)}}\)，这个式子保证了当\(Z(W)\to 0\)时，\(I(W)\to 1\)；
\(I(W)\leq\sqrt{1-Z(W)^2}\)，这个式子保证了当\(Z(W)\to 1\)时，\(I(W)\to 0\)。

3.2 证明过程#

之所以额外引入了一个参数\(Z(W)\)，是因为在节点分裂\((W,W)\to(W',W'')\)的过程中，关于\(I(W),I(W'),I(W'')\)我们只能知道一个模糊的大小关系：

\[I(W') \leq I(W) \leq I(W'')\]

而关于\(Z(W),Z(W'),Z(W'')\)我们不仅有相似的大小关系：

\[Z(W'') \leq Z(W) \leq Z(W')\]

还有一个明确的计算公式：

\[Z(W'')=Z(W)^2\]

不过可惜的是，相比\(I(W)\)条件期望保持不变的优良特点，\(Z(W)\)在分裂后会变小（从而只能构造出一个上鞅，supermartingale）：

\[Z(W')+Z(W'')\leq 2Z(W)\]

因此Arikan的论证思路是，根据\(I(W)\)和\(Z(W)\)之间的关系，分别使用\(I(W)\)证明收敛性、以及使用\(Z(W)\)证明收敛后的随机变量取值于\(\{0,1\}\)：

基于对称容量构造一个鞅\(\{I_n\}\)，根据鞅收敛定理知道，当\(n\)趋于无穷时，它几乎处处收敛到一个随机变量\(I_\infty\)；
基于Bhattacharyya参数构造一个上鞅\(\{Z_n\}\)，根据鞅收敛定理知道，当\(n\)趋于无穷时，它几乎处处收敛到一个随机变量\(Z_\infty\)，且\(Z_\infty\)取值于集合\(\{0,1\}\)；
根据\(I(W)\)和\(Z(W)\)之间的关系，知道\(I_\infty\)也取值于集合\(\{0,1\}\)。

这一过程在原文中为：

Arikan的证明过程

想要了解更多证明细节，请直接阅读原文，任何第三方资料都没有原文更权威。