四、如何译码?#
1. 信道的输出信息#
在介绍极化码的译码算法之前,必须先建立关于“信道”这个数学对象的基本认知。例如,对于一个比特翻转概率为\(p\)的信道,如果在某次使用过程中,信道输出比特\(1\),请问输入的原比特可能是多少?
解答:若记输入的随机变量为\(X\),输出的随机变量为\(Y\),那么根据Bayes公式:
我们实际是求条件概率:
其中\(x\in\{0,1\}\)。如果输入的随机变量\(X\)是均匀分布,那么上式将退化为比较简单的信道转移概率:
从数学上来讲,虽然信道只输出了一个比特\(1\),但我们可以获取的完整信息远不止如此,结合我们关于信道的认知,可以进一步求出关于输入随机变量\(X\)的条件概率分布\(\Pr(X=x|Y=1)\)。显然这样一种“软”的结果包含了更多的信息,有利于获取更好的通信性能。在现代研究中,除了存在特殊的硬件限制外,我们将总是使用软译码策略。
极化码也存在比特翻转等硬译码算法,但性能不如LDPC,除理论研究外很少考虑。
为了令信道纠错码的译码器可以方便地获取Bayes条件概率,这部分计算负担往往由通信接收方的解调器承担,即执行所谓的“软判决”。对于二进制情况,我们定义对数似然比(Log-Likelihood Ratio)为:
不难发现,它是关于条件概率分布\(\Pr(X=x|\text{Some Condition})\)的充分统计量,在知道对数似然比后,我们可以立即计算\(x=0\)和\(x=1\)对应的条件概率,而不会出现混淆。出于这种良好性质,在许多二进制纠错码研究工作中,都会选用对数似然比描述它们的译码算法。
非二进制纠错码不存在似然比,只能使用条件概率分布进行译码。
2. 最小和SC译码#
为了尽量避免劝退的复杂公式,我们将首先描述最小和译码算法。该译码算法简单到令人怀疑其正确性,其设计初衷也是为了提高硬件计算效率。关于正确性的理论推导,将推迟到后续章节介绍。
2.1 码长为2的极化码#
码长为2的极化码结构如下图所示:
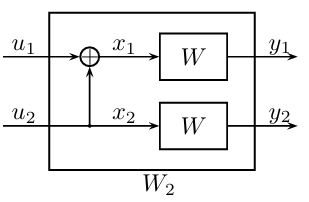
容易知道,其码率只有\(R=1/2\)一种,冻结位是\(u_1=0\),发送端只能在\(u_2\)上传输信息比特。不论信道是翻转信道、擦除信道还是AWGN信道,我们总能在接收到\(y_1\)和\(y_2\)之后,计算对应的\(x_1\)和\(x_2\)的对数似然比,分别记作\(L_1\)和\(L_2\),那么在已知信道的统计特征、以及\(y_1\)、\(y_2\)和\(u_1\)的值的条件下,比特\(u_2\)的对数似然比为:\(L_1 + L_2\)。
2.2 码长为4的极化码#
码长为4的极化码结构如下图所示:
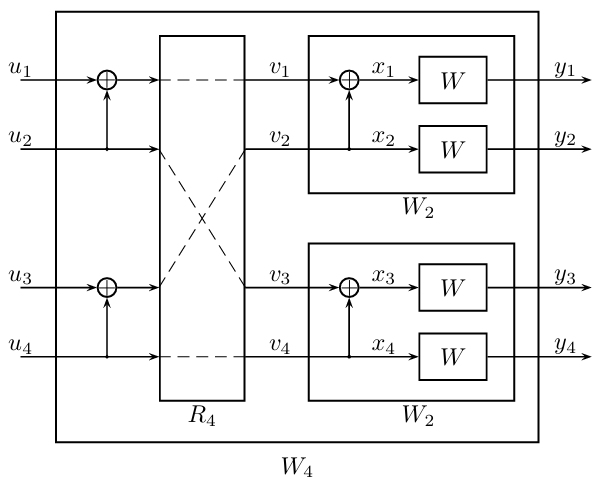
当码长稍微增加一些时,事情突然变得十分复杂。即便预设一个固定的冻结集,比如令\(u_1=u_3=0\),我们也难以将上述码长为2的情况直接推广到这里。比如,在已知\(x_{1:4}\)的对数似然比分别为\(L_{1:4}\)的情况下,没有手段求出\(v_{1:4}\)的似然比,也就无从谈起求\(u_2和u_4\)的似然比。我们需要对码长为2的极化码做更多的讨论。
2.3 码长为2的极化码(三种子运算)#

① 已知\(L^x_1,L^x_2\),求\(L^u_1\):\(L^u_1 = \text{sign}(L^x_1) \times \text{sign}(L^x_2) \times \min \left\{|L^x_1|, |L^x_2|\right\}\)
② 已知\(L^x_1,L^x_2\)和\(u_1\)的值,求\(L^u_2\):\(L^u_2 = (1 - 2u_1) \cdot L^x_1 + L^x_2\)
③ 已知\(u_1,u_2\)的值,求\(x_1,x_2\)的值:\(x_1=u_1+u_2,x_2=u_2\)
2.4 码长为\(N=2^n\)的极化码(连续消除规则)#
在定义了上述三种运算之后,我们进一步地规定一个译码顺序:连续消除(Successive Cancellation)。
具体来说,译码过程是从右到左逐层进行的,在每一层中,对所有码长为2的极化码子结构,都应当先执行运算①,然后再跳转到下一层,继续根据目前已知的似然比(数量已减半)递归地执行子运算①,直到计算到最左一层的\(u_1\)后,我们对它进行判决,得到一个确定的值,接下来就可以执行子运算②计算并判决\(u_2\),然后我们根据这两个确定的值使用子运算③跳转到上一层。此时在这一层我们会获得一些更新后的值,使得我们可以执行子运算②。通过这样一种类似二叉树左序遍历的过程,最终可以实现完整的译码。
上面的叙述比较抽象,我们看一个具体的例子,在序列\(u_{1:4}\)中冻结\(u_1=0\),其他位传输信息,则某次译码过程如下:
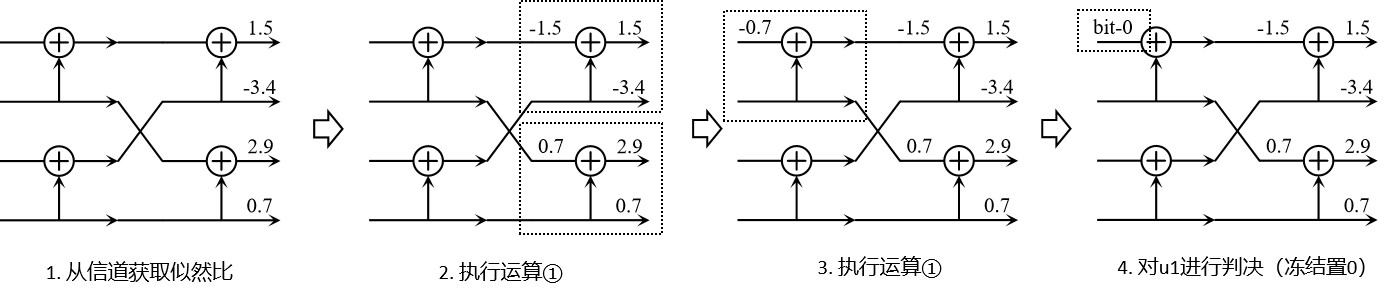
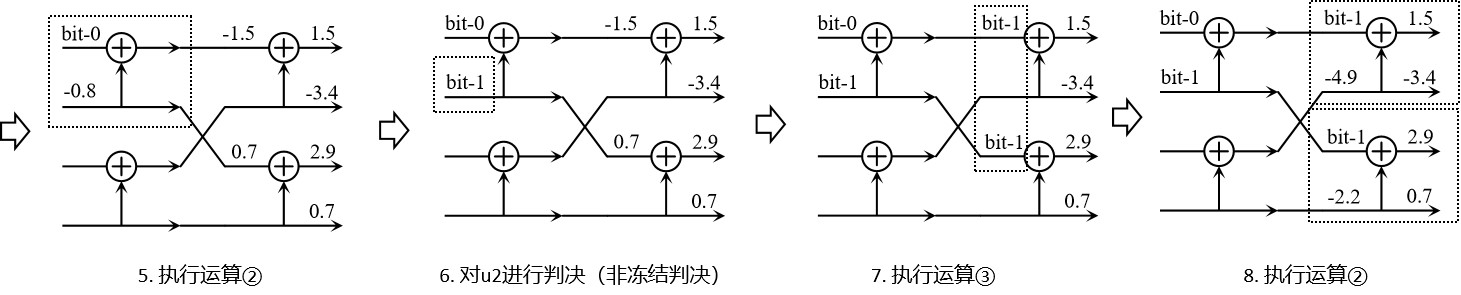

上面这个例子很容易推广到\(N=2^n\)码长情况下,不做赘述。至于连续消除规则背后的原理,它涉及极化码的根基,不可能在短篇幅内解释清楚,你在这里只需要强制认同它。如果你是深度研究者,推荐阅读Arikan曾提出的一种用于进行Slepian-Wolf编码的单调链极化码(Monotone Chain Polar Codes),其中采用了所谓的单调消除规则,或许可以开拓你的研究思路。
本手册的对应库中,plcoding.cpp_core.iterator中的PolarIterator对象支持任意顺序译码,可用于支持更深入的理论研究。
